Project
Details
More project information.
Shared data and results available are linked.
Sensitivity analysis over North America
Streamflow sensitivity to different hydrologic processes varies in both space and time. In numerical modeling of streamflow, this sensitivity manifests as parameter sensitivity, which is typically model-specific. In this study, we apply a novel analysis over more than 3000 basins across North America enabling the estimation of the process sensitivities on streamflow based on basin characteristics that can be derived from physiographic and climatologic data without needing to perform the expensive sensitivity analysis itself. This allows for high-level conclusions as to the importance of water cycle components on streamflow predictions, as the analysis considers a flexible model structure rather than an individual model. This work derives the sensitivity of streamflow simulation to entire hydrologic processes rather than only specific parameters. Process sensitivities are computed and provided for each day of the year over a wide range of physiographic and climatologic regimes, enabling future hydrologic model improvement at the continental scale.
This work has been published (here). The codes and data are available on GitHub and are published under Zenodo. Please refer to the following reference when citing this work:
J. Mai, J. R. Craig, B. A. Tolson, and R. Arsenault (2022).
The Sensitivity of Simulated Streamflow to Individual Hydrologic Processes Across North America.
Nature Communications, 13(1), 455.
(link)
-

Physiographic basin properties
The following map will display the aggregated physiographic information for each watershed in the database. The properties are derived from the HydroSHEDS (2006) dataset. The void-filled HydroSHEDS digital elevation model (DEM) with a 30 arcsec resolution is used and can be downloaded for free (here). The information was extracted with the PAVICS subsetting tools.
The map includes switches to display the following properties: latitude of watershed centroid [deg], longitude of watershed centroid [deg], area [km2], elevation [m], slope [deg], gravelius [frac], perimeter [km], aspect [deg].
The blended Raven model used for the hydrologic simulations used the properties of area, elevation, slope, as well as latitude and longitude of the watershed centroid. -

Landcover related basin properties
The following map will display the aggregated landcover information for each watershed in the database. The landcover information was derived from the NALCMS (250m, 2010) dataset. The datset can be downloaded for free (here). The information was extracted with the PAVICS subsetting tools using the zonal histogram methods and spatially aggregated using the percentage of NALCMS tiles of each group within the catchment polygon.
The map includes switches to display the fractions of forest (NALCMS class 1 to 6), grass (NALCMS class 9, 10 to 13, and 16), wetland (NALCMS class 14), water (NALCMS class 18), urban (NALCMS class 17), shrubs (NALCMS class 7, 8, and 11), crops (NALCMS class 15), snow-ice (NALCMS class 19), ocean not displayed since zero everywhere on land (NALCMS class 0). All landcover values are fractions and range between 0 and 1. The definitions of these classes can be found here.
The blended Raven model used for the hydrologic simulations only requires the estimate of the forest fraction. -

Knoben climate indicators
The climate indicators are based on Knoben et al. (2018). The climate indicators aridity Im, seasonality Im,r, and precipitation as snow fS are estimated using daily precipitation, avergage daily temperature, and potential evapotranspiration of the watershed. The three indicators are used to derive a color which is used to identify the continuous climatic zones. The indicators have the following ranges: aridity (arid to wet) within [-1,1], seasonality (constant to seasonal) within [0,2], and precipitation as snow (no snow to all snow) within [0,1].
The RGB color derived from these indicators is defined as follows: aridity (red), seasonality (green), and precipitation as snow (blue). The following map allows you to display the three climate indicators as well as the color proposed by Knoben et al. (2018) that is indicating the climatic zone (Fig. 2 in Knoben et al. (2018)). -

Calibration results
We performed a calibration of basins in North America using stations in Canada retrieved from Water Survey Canada (WSC) and in the United States retrieved by from the United States Geological Survey (USGS). Our simulation period is January 1991 to December 2010 with the 2 prior years regarded as warm-up. We selected only stations that had at least 5 years observed streamflow available during this 20 year period. In total 3826 stations are calibrated.
We used the Ostrich calibration toolbox for calibrating the model. The Dynamically Dimensioned Search (DDS) algorithm with a budget of 2000 model eveluations was employed to maximize the Nash-Sutcliffe Efficiency (NSE). We performed 10 independent trials (each 2000 evaluations) and report the best results. The setups can be downloaded by clicking on the watershed on the main page and select "calibrated model setup (zip)".
The following map will report NSE (calibrated) as well as the Kling-Gupta Efficiency (KGE) and the Root-Mean-Square Error (RMSE). The latter two are not calibrated but derived using the run leading to the best Nash-Sutcliffe efficiency. Be aware that the RMSE are absolute estimates; they are not normalized regarding basin area etc. -

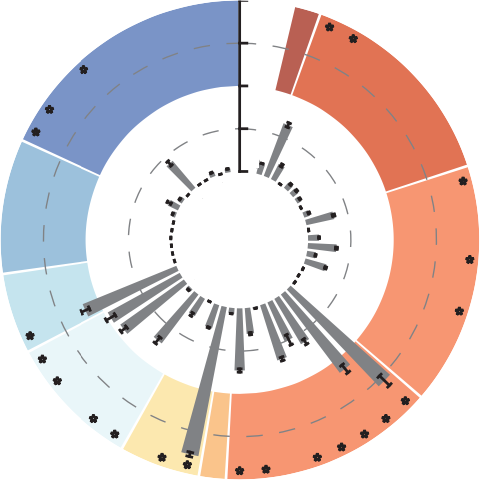
Time-dependent total Sobol' sensitivity indexes
The plot on top is showing the results of the Sobol' sensitivity analysis of the hydrologic modeling framework Raven. The sensitivities of eleven processes are shown as their averages per day of the year (colored bars). The simulation period is 1991 to 2010 while the first two years are discarded as warm-up period. The sensitivities are normalized such that they sum up to 1.0 at every day of the year. The sensitivities are variance-weighted averages. The (average) weight of each day of the year is shown in the plot below (black line). The weights for every time step are determined by the average simulated discharge at this time step.
-

Aggregated total Sobol' sensitivity indexes
The following map will give you an overview on the sensitivity of eight hydrologic processes and three input corrections across all watersheds in North America analyses. The processes considered here are infiltration, quickflow, evaporation, baseflow, snow balance, convolution of surface runoff, convolution of delayed runoff, and percolation. The three input corrections are potential melt, rain-snow partitioning, and precipitation correction.
The indexes displayed are the variance-weighted time-aggregated total Sobol' sensitivity indexes regarding streamflow simulated using the blended Raven model based on HMETS (panel C in the figure below). The simulation period is 1989 to 2010 while the first two years are discarded as warm-up period. The weights for each time step of the streamflow time series are derived using the variance of all simulations at the given time step.
 hydrohub
hydrohub